1前言
可拓学在迅速发展中,其基础理论和应用研究都取得了长足的进步,人们对其基本概念和理论框架的认识也逐步深入。因此,经常地总结可拓学的研究成果就显得十分必要。
任何学科的形成和发展过程,都是该学科的日益完善、精确化的过程。学科基本概念日臻精确,标志着该学科的日益成熟。近年,可拓学在基本概念和基本理论方面,有逐步精确和深入的倾向,及时地总结这些成果有助于可拓学的进一步发展。
笔者简要介绍近年来,在可拓学的基本概念和基础理论研究方面取得的新进展,供广大可拓学研究者参考。
2 关于可拓学的理论框架
可拓学是用形式化模型研究事物拓展的可能性和开拓创新的规律与方法,并用于解决矛盾问题的科学[1~7]。
可拓学的研究对象是客观世界中的矛盾问题。
可拓学的逻辑细胞是基元,包括物元、事元[8]和关系元。
可拓学的逻辑基础是可拓逻辑。
可拓学的基本理论是可拓论,可拓论由基元理论、可拓集合理论和可拓逻辑作为其三大支柱。其理论框架如图1所示。
可拓学特有的方法是可拓方法,包括可拓分析方法、可拓变换方法和可拓集合方法等。
可拓论与可拓方法应用于各个专业领域的技术,称为可拓工程[9]。
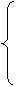
[收稿日期]2002-08-09;修回日期:2002-09-26
[基金项目]国家自然科学基金资助项目(70140003),广东省自然科学基金资助项目(010049)
[作者简介]蔡文(1942—),男(汉),广东澄海市人,广东工业大学研究员,国家级有突出贡献专家

图1可 拓 论 框 架
Fig.1 The Framework of Extension Theory
3 关于基元理论
可拓学研究解决矛盾问题的理论和方法。它与其他学科对矛盾问题的研究不同之处在于使用了形式化的模型,运用了可拓变换和可拓推理的方法。要利用形式化方法处理客观世界中各种矛盾问题,首先必须研究如何描述客观世界中的各种事物。
客观世界中,物的各种特征描述了它的各个侧面,万物及其相互联系构成了世界的静态结构。另一方面,万物之间的相互作用使它们处于运动和变化之中,物与物之间的相互作用称为事。物、事以及它们之间的关系,构成了五彩缤纷、变化万千的动态世界。要研究问题,就要从研究物、事和关系的各个侧面开始,通过对它们的分析,找到解决矛盾问题的方法。
3.1 基元
3.1.1 物元一物具有多个特征。这些特征由特征的名称及相应的量值所构成。
定义1把物N、特征名c和N关于c的量值v构成的有序三元组
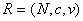
作为描述物N的基本元,称为一维物元。其中c和v构成的有序二元组
M=(c, v)
表示物N的一个特征。
由物N和它的多个特征Mi=(ci, vi)构成的物元称为多维物元[4]。
物是随时间t变化的,可用动态物元
R(t)=(N(t),c,v(t))
来描述。类似地,物也随空间位置和其它条件的改变而改变。为此,上式中的t可视为一般参数,以带t的参变量物元R(t)来表示物和特征随参数的改变而改变。
定义2在物元R=(N,c,v)中,若N,v是参数t的函数,称R为参变量物元,记作
R(t)=(N(t),c,v(t))。
这时,v(t)=c(N(t))。为了书写方便起见,在不引起混淆的地方,省略参数t,简记为v=c(N)。
3.1.2 事元物与物的相互作用称为事,事以事元来描述。
定义3把动词、动词的特征名及相应的量值构成的有序三元组作为描述事的基本元,称为一维事元,记作
I=(动词,动词的特征名,量值)=(d,h,u)
对动词而言,它的基本特征名有:支配对象、施动对象、接受对象、时间、地点、程度、方式、工具。由动词和它的多个特征名及相应的量值构成的事元,称为多维事元[8]。
定义4在事元I=(d,h,u)中,若d和u是参数t的函数,则称I为参变量事元,记作
I(t)=(d(t),h,u(t))
在事元概念中,u(t)=h(d(t))反映了动作和量值的关系。为书写方便,在不致引起混淆的情况下,记为u=h(d)。
定义5给定事元I1=(d1,h1,u1)和事元I2=(d2,h2,u2),称I1=(d1,h1,I2)为复合事元。
定义6给定物元R=(N,c,v)和事元I=(d,h,u),称R=(I,c,v)和R=(N,c,I)为物事元,称I=(d,h,R)为事物元。
3.1.3关系元为了描述物与物,事与事及物与事的关系,引进关系元的概念。
定义7(关系元)把关系词或关系符(简称关系名)、关系的特征名及相应的量值构成的有序三元组作为描述关系的基本元,称为一维关系元,记作
Q=(关系名,关系的特征名,量值) =(s,a,z)
对关系而言,它的基本特征名有:前项,后项,密切程度,维系工具,通道,方式,联系频率,地点等。
定义8在关系元Q=(s,a,z)中,若s和z是某参数t的函数,则称Q为参变量关系元,记作
Q(t)=(s(t),a,z(t))
当t为时间参数时,称Q(t)为动态关系元。
定义9(n维关系元)以关系名s,它的n个特征名a1,a2,…,an和相应的量值z1,z2,…,zn构成的n维阵列
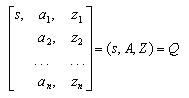
来描述z1和z2的关系,称为n维关系元,其中
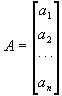 ,
,
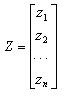
特征名a1,a2,…,an可以是前项,后项,密切程度,维系工具,通道,方式,联系频率,地点等,z1,z2,…,zn是相应于各特征名的量值。
3.1.4以基元表示的模型
在可拓学中,建立了以物元、事元和关系元为基本元的形式化体系,物元

,事元

和关系元

,是描述千变万化的大千世界的基本元,统称为基元。它们可以简洁地刻划客观世界中的事、物和关系,也可以为计算机所接受。基于这种形式化体系来表示信息、知识和问题等的模型,可以把世界看成一个物元网[10]。事视为物元网中物元的相互作用。关系元刻划物元和物元、物元和事元、事元和事元之间的相互关系。这种模型不仅研究事物的数量关系,还考虑事物的质的方面。
在可拓学中,利用基元可以形式化地描述矛盾问题,把问题分为目标和条件两部分,并用基元加以表示。继之,建立物元可拓集合、事元可拓集合或关系元可拓集合,用基元在可拓集合中的负域或正域来描述矛盾和相容,用关联函数值的大小来衡量矛盾的程度或相容的程度,以关联函数值的变化来表示事物的量变或质变。
利用基元表示的模型,可以简洁地描述信息和知识。在人工智能已有的分支和知识表示体系中,信息和知识的表示各有特点,但以基元表示的模型可为人工智能提供一种简洁规范的知识表示方法。
另一方面,基元理论研究事物和关系的可拓性。信息和知识用基元描述以后,可以利用基元的可拓性,开拓出新的信息和知识,为人工智能的策略生成技术提供依据;为信息开发和知识挖掘提供理论和方法。可拓信息和可拓知识库的研究正是把基元表示的模型应用于人工智能的一种尝试。
3.2可拓分析理论
可拓性是事物固有的特性。整个世界,包括客观世界和主观世界,都存在可拓性,人类要进一步认识世界和改造世界,就要认识事物的可拓性,了解进行开拓的可能性。对事物的可拓性认识越清楚,越能提出解决矛盾问题的变换,越能使用更可行的方法、窍门和点子,去处理开拓过程中出现的种种矛盾问题。可拓性的研究,使人的开拓活动更有规律可寻、更有理论可依。物的可拓性是多种多样的,事的可拓性和关系的可拓性也是多种多样的,因此,开拓的可能性有多种。人们可以借助计算机找到解决矛盾问题的多种方案。
世界的可拓性,既包括了客观世界中各种事物的可拓性,也包括了人的可拓性以及各种关系的可拓性。事物的可拓性为人们解决矛盾问题提供了各种开拓的可能性,因此,研究事物的可拓性是一个十分重要的课题。如果说,开拓是人类社会发展的主旋律,那么,物、事和关系的可拓性就是开拓的依据。
可拓分析理论就是研究基元拓展的可能性的理论。它包括物元分析理论、事元分析理论、关系元分析理论和复合元分析理论。
3.3共轭分析理论
共轭性是物具有的特性。物的共轭性是从物质性、系统性、动态性和对立性四个角度研究物的结构,从而把物分为虚部和实部、软部和硬部、潜部和显部、负部和正部,记为
N= imNÄreN= sfNÄhrN= ltNÄapN= ngcNÄpscN
大量的奇谋妙计产生于虚部、软部、潜部和负部的开拓,利用共轭性可以为产生解决矛盾问题的点子、窍门和办法提供依据。
利用共轭性,可以对资源进行分析,把资源分为虚资源和实资源、软资源和硬资源、潜资源和显资源、负资源和正资源,从而为微观到宏观的策划提供多种可用的资源[11]。
利用共轭性,对产品进行分析,可以把产品分为虚产品和实产品、软产品和硬产品、潜产品和显产品、负产品和正产品。这些产品的出现是基于人的需要而产生的,人的需要可以分为虚需要和实需要、软需要和硬需要、潜需要和显需要、负需要和正需要[12]。
总之,共轭分析理论为人们提供了一种新的思考方式去研究问题和处理问题。
3.4可拓变换理论
可拓学研究初期,提出了物元变换,随着事元和关系元的引入,相应地研究了事元变换和关系元变换。物元变换、事元变换和关系元变换统称为基元变换。在可拓集合理论的研究中,我们发现,要解决矛盾问题(即把问题的相容度从负值变为正值),除了元素本身变换以外,还可以使用关联准则的变换。后来,又发现,还可以通过论域的变换来实现。因此,可拓变换包括如下类型的基本变换:
4 关于可拓集合
事物的矛盾性是可变的,随着环境、条件和时间的变化而变化,特别是随人们采取不同的变换而改变。
如上所述,为了解决矛盾问题,人们利用了各种变换,使矛盾转化为相容。而描述这一过程的定量化工具的基础是可拓集合论。
集合,是现代逻辑学的基础之一。
可拓集合是可拓学中用于对事物进行动态分类的重要概念,也是可拓学用于解决矛盾问题、形式化描述量变和质变的基础。利用可拓集合可以对市场、资源、控制、检测等领域中“不行变行”、“不是变是”、“不知变可知”的过程进行形式化描述、推理与变换,从而得到解决矛盾问题的策略的定性部分和定量部分。
可拓集合的概念是在经典集合和模糊集合的基础上发展起来的。由于经典集合和模糊集合较少考虑论域中事物本身及其性质的可变性,从而使得很多矛盾问题无法用数学方法去解决,可拓集合正是基于这种需要而提出的。
文献[2]中用一元组建立了可拓集合的初步定义,文献[7]引进了变换T,用二元组来规定可拓集合,并规定了可拓集合把论域划分为正域、负域、零界、可拓域、稳定域等,其中用两个定义一起来描述元素的可变性及量变和质变的过程,使描述更为清晰、准确,但从可拓集合的第一个定义难以直接反映出“是”与“非”的相互转化,而且,第二个定义中涉及到的变换T也只是对元素的变换。文献[4]中又将变换T扩展到对关联函数和对论域的变换。
为了概括十多年来关于可拓集合的研究成果,使可拓集合的定义能直接描述元素性质的可变性和量变、质变的过程,笔者用三元组(u,y,y’)和可拓变换T=(TU,Tk,Tu)来规定可拓集合[13~15]。
定义10设U为论域,k是U到实数域(-∞,+∞)的一个映射,T为给定的对U中元素的
变换,称

(T)={ (u,y,y’)∣u∈U,y=k(u)∈(—∞,+∞),y’=k(Tu)∈(—∞,+∞) }
为论域U上关于元素变换T的一个可拓集合,y=k(u)为

(T)的关联函数。
1)当T=e(e为幺变换)时,记

(e)=

={ (u,y)∣u∈U,y=k(u)∈(—∞,+∞) },此即文献[7]所定义的可拓集合。此可拓集合可划分为三部分:
A={ (u,y)∣u∈U,y=k(u)≥0 }
称为

的正域;

={ (u,y)∣u∈U,y=k(u)≤0 }
称为

的负域;
J0={ (u,y)∣u∈U,y=k(u)= 0 }
称为

的零界。
2)当T≠e时,把

+(T)={ (u,y,y¢)∣u∈U,y=k(u)≤0 ,y¢=k(Tu)≥0}
称为

(T)的正可拓域;

-(T)={ (u,y,y¢)∣u∈U,y=k(u)≥0 ,y¢=k(Tu)≤0}
称为

(T)的负可拓域;
A+(T)= { (u,y,y¢)∣u∈U,y=k(u)≥0 ,y¢=k(Tu)≥0}
称为

(T)的正稳定域;
A-(T)={ (u,y,y¢)∣u∈U,y=k(u)≤0 ,y¢=k(Tu)≤0}
称为

(T)的负稳定域。
J0(T)={ (u,y,y¢)∣u∈U,y¢=k(Tu) =0}
称为

(T)的拓界。
在上述关于元素变换的可拓集合中:
1)当T=e时,把论域U对应划分为三部分:
V={u∣u∈U,y=k(u)≥0 }
称为论域U关于

的正域,简称正域。

={u∣u∈U,y=k(u)≤0 }
称为论域U关于

的负域,简称负域。
J0={u∣u∈U,y=k(u)= 0 }
称为论域U关于

的零界,简称零界。
2)当T≠e时,把论域U对应划分出关于变换T的正负可拓域、正负稳定域和拓
界五部分,其中

+(T)={u∣u∈U,y=k(u)≤0 ,y¢=k(Tu)≥0}
称为论域U关于T的正可拓域,简称正可拓域;

-(T)={u∣u∈U,y=k(u)≥0 ,y¢=k(Tu)≤0}
称为论域U关于T的负可拓域,简称负可拓域;
V+(T)={u∣u∈U,y=k(u)≥0 ,y¢=k(Tu)≥0}
称为论域U关于T的正稳定域,简称正稳定域;
V-(T)={u∣u∈U,y=k(u)≤0 ,y¢=k(Tu)≤0}
称为论域U关于T的负稳定域,简称负稳定域。
J(T)={u∣u∈U,y¢=k(Tu) =0}
称为论域U关于T的拓界,简称拓界。
图2关于元素变换的可拓集合对论域的划分
Fig.2 The Partition of the Universe in Extension Set with respect to the Element Transformation
在定义10的基础上,可以建立关于关联准则和论域的变换的可拓集合以及一般可拓集合的定义,请参阅文献[14]。
由上述定义可见,可拓集合用(–∞,+∞)中的数来描述事物具有某种性质的程度,并描述了事物“是”与“非”的相互转化,它既可用来描述量变的过程(稳定域),又可用来描述质变的过程(可拓域)。零界和拓界描述了质变点,超越它们,事物就产生质变。
可拓集合的核心概念是可拓域[16]。可拓域有正可拓域和负可拓域之分。正可拓域描述了经典集合的非域或论域外一部分元素,它们不具有某种性质,但由于可拓变换(包括元素本身的变换,关联函数的变换和论域的变换),变为具有该性质。显然,不同的变换具有不同的可拓域。可拓域中的元素,经过变换产生了质变。可拓域的提出,使把矛盾问题转化为相容问题具有合理的集合论基础。
与可拓域相反的是稳定域,它描述了在变换T下,其性质不产生质的变化的元素。事物的变化在稳定域内进行的,属于量变的范围。
如上所述,可拓集合有两条疆界,一条是零界,一条是论域的边界。论域的变换表现为它的边界的改变,关联准则的变换表现为正域和负域的分界——零界的改变,元素的变换是物、事、关系或它们某些特征的改变,也即物元、事元或关系元的变换。通俗地说,可拓变换可表现为两疆及元素的变换。这里特别一提的是,(–∞,+∞)与(-1,+1)是同构的,有的文章建议采用(-1,+1)作为关联函数的取值范围。这只要经过一个映射就行了。
为了描述论域是多元的情况,建立了n元可拓集合和n维可拓集合的概念。
定义11设

,


,

称

(T)={

|


∈(-∞,+∞),

∈(-∞,+∞)}
为U上的一个n元可拓集合,其中T=(TU,Tk,Tu),

,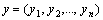 ,
,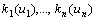
定义12设

,

,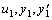
 ,
,

={(

)|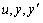
 ∈(-∞,+∞),
∈(-∞,+∞),
 ∈(-∞,+∞)}
∈(-∞,+∞)}
称
 (T)={(
(T)={(

)|


∈(-∞,+∞),

∈(-∞,+∞)}
为U上的一个n维可拓集合。其中T=(TU,Tk,Tu)


,


5 关于可拓逻辑
5.1可拓逻辑的研究背景
要使计算机能利用基元表示的模型处理矛盾问题,生成解决矛盾问题的策略,必须研究带有矛盾前提的逻辑。
可拓逻辑是研究把矛盾问题转化为不矛盾问题的推理规律的科学,它是继基元理论和可拓集合理论之后提出的,成为可拓论的第三个支柱。可拓逻辑是异于数理逻辑和模糊逻辑的逻辑。它将为计算机处理矛盾问题提供依据。
在人类处理各种问题的过程中,根据事物的可拓性,提出了种种可以开拓的途径,进行了多种失败和成功的尝试,找到解决问题的方法,使人类进行了生存空间的开拓,生产方式的开拓,生产工具的开拓…。直到今天,人类还在不断地向微观和宏观开拓,向智能化开拓…。在人类的发展史中,人把事物看成是可以拓展的,利用这种思想去处理人类发展过程中的种种问题。我们把这种思维方式称为可拓思维方式。研究可拓思维方式,将有利于总结人类开拓的历史,为今后的开拓提供合理的理论和方法。
可拓学研究的初期,重点在于建立描述客观世界中的物、事和关系的基本元,提出了物元、事元和关系元等概念,建立了可拓集合和关联函数等定量化工具。理论研究发展到今天,需要把重点从模型的建立转移到对变换、判断和推理的研究上。另一方面,目前可拓学的应用研究是十分初步的,不少学者感到“工具不足”,这迫切要求可拓学理论工作者研究可拓论与专业领域相结合的“变换”和“推理”工具。由此可见,无论从可拓学的理论研究出发,还是从应用研究考虑,研究可拓思维方式的规律,探讨符合可拓思维方式的变换、判断和推理形式必然成为今后可拓学研究的重点之一。
5.2可拓逻辑的特点
可拓逻辑是异于形式逻辑和辩证逻辑的逻辑,它有如下几个特点:
1) 研究化矛盾为相容的逻辑
数理逻辑主要研究没有矛盾前提的逻辑。但是,人们天天要与矛盾打交道,天天要处理各种各样的矛盾问题。因此,人们不但要研究非矛盾的逻辑,还要研究带有矛盾前提的逻辑。可拓逻辑正是研究如何化矛盾为相容的逻辑。通俗地说,它研究如何在矛盾前提下,通过某些变换,得到相容的结论。
数理逻辑研究经典数学中推理的规律,模糊逻辑研究模糊数学中推理的规律,可拓逻辑研究可拓学中推理的规律。由于经典数学研究的是确定性的问题,模糊数学研究的是模糊性的问题,可拓学研究的是矛盾问题。因此,它们对应的逻辑随研究对象的不同而不同。
当然,可拓逻辑也研究不带矛盾前提的逻辑,也即变换是幺变换的逻辑。这时,可拓逻辑就蜕化为经典逻辑或模糊逻辑。可以说,可拓逻辑是在经典逻辑和模糊逻辑基础上发展起来的一种新的逻辑。
2) 逻辑值随变换而改变
在经典逻辑中,事物是否具有某种性质,只取“是”与“非”;命题是否正确,只取“真”与“假”,即特征函数值只取0或1。而在模糊逻辑中,隶属度取值[0,1]中的实数。但在可拓逻辑中,用取自(-∞,+∞)(与(-1,1)同构)的实数来描述“是”与“非”以及“真”与“假”的程度。这种程度可正可负,正值表示“是”或“真”的程度,负值表示“非”或“假”的程度。从而,把“类内为同,类间为异”发展为“类内也有异”,即类内也有程度的区别[17]。
在经典逻辑和模糊逻辑中,事物是否具有某种性质,命题为“真”或为“假”是相对固定的。但在可拓逻辑中,由于引入了变换(包括时间和空间的改变),事物具有某种性质的程度和命题“真假”的程度随变换而改变。可以说,经典逻辑和模糊逻辑从“静态”的角度研究事物的性质和命题的真假;可拓逻辑则从“动态转化”的角度讨论事物具有某种性质的程度和命题真假的变化。
3) 形式逻辑的形式和辩证逻辑的思想
“传统名词逻辑的基本观点就是以非空非全的类作为认识世界的着眼点,只注意类与类之间的关系,而忽视组成类的个别事物即个体,忽视个体与个体之间的关系。谓词逻辑则以个体作为认识世界的着眼点。¼¼以一定论域中的一切个体作为对象,研究它们的一般性质和关系,以达到认识世界的目的,这就是谓词逻辑的基本观点。”[18]可拓逻辑则是以个体的特征及个体的内部结构作为认识世界的着眼点。以基元作为描述工具,研究它们的一般性质和关系,以达到认识世界的目的。因此,可拓逻辑不仅研究类和个体,还研究描述个体的特征和个体的共轭部,即研究物元、事元、关系元和共轭部。
可拓逻辑中,以基元在可拓集合中的位置作为描述事物矛盾程度的依据,也作为描述矛盾问题相容度的依据
可拓逻辑要研究“变”的推理规律,就必须符合自然辩证法的基本规律[19]。因此,可拓逻辑也进行了哲学原理形式化的尝试。通过用符号对某些哲学原理进行描述,可以对这些规律进行操作和运算,使辩证逻辑不仅仅停留于自然语言的描述。
可以说,可拓逻辑汲取了形式逻辑形式化的做法,采用了辩证逻辑的思想,结合并发展出描述可拓思维形式,以化矛盾为相容的逻辑。
5.3可拓逻辑的内容
可拓逻辑的研究内容主要有如下三个方面:a.概念的可拓表示和可拓概念;b.命题的可拓模型和可拓命题;c.推理的可拓模型和可拓推理。在上述基础上,研究了矛盾问题的可拓模型和解决矛盾问题的可拓逻辑.
5.3.1概念的可拓表示和可拓概念
概念的可拓表示和可拓概念是研究可拓思维形式的基点。概念是反映对象的一般本质、内部联系和发展规律的思维形式。在形式逻辑中,把概念看成思维的逻辑细胞,它是构成其它思维形式的基本要素。形式逻辑撇开概念的具体内容,只在形式结构上研究概念,从概念外延的角度研究概念之间的关系。而在辩证逻辑中,却密切结合概念的具体内容和概念的运动变化来研究概念。一个概念的内涵越丰富,用以揭示的判断就越多;而关于推理,则看成判断的分化与展开。
可拓逻辑既考虑概念的外延,也考虑概念的内涵,物元和事元是描述概念内涵的简明形式。而关系元则描述了概念外延之间的关系。因此,基元也都是判断的简洁描述形式。基元的维数越多,所描述的概念内涵也越多,从而所描述的判断也越多。
可拓概念是对概念之间的关系的一种描述形式。利用可拓概念可以把概念的内涵和外延之间的关系结合起来。
5.3.2命题的可拓模型和可拓命题
形式逻辑把判断(或命题)看作是概念的结合,把推理看作是判断(或命题)的结合。因而在形式逻辑(或数理逻辑)体系中,概念是构成判断和推理的基本单位。而在辩证逻辑中,命题、推理主要不是概念间的联结,而是概念内在矛盾的展开。判断就是对概念加以内在的区别和规定。任何事物都具有多方面的规定性,即具有多种属性。人们对某类事物下判断,总是从某一特定方面去做判定。在可拓逻辑中,物元R=(N,c,v)可以描述概念N的一个命题,n维物元可以描述概念N的n个命题。这时,物元可以看成是对概念N的内涵的描述,是概念N的展开,一物多征是N的多方面展开。可拓逻辑利用基元描述命题[20],利用可拓集合描述命题的真假程度。
命题用基元描述以后,由于基元的可拓性,可以生成很多新的命题,即可拓命题。命题的可拓模型、可拓命题和命题变换的研究,为利用计算机表示命题、进行命题运算提供了新的工具[21]。为描述自然语言和机器翻译的研究提供新的方法。
5.3.3推理的可拓模型和可拓推理
在形式逻辑中,推理是命题的结合。而在辨证逻辑中,推理乃是判断的分化和展开。可拓逻辑以基元形式化表示命题,把可拓推理作为命题的进一步分化和展开。
推理技术是人工智能的重要技术,它研究前提和结论之间的各种逻辑关系及真度的传递规律等。现有人工智能的推理系统,不少是建立在形式逻辑的基础之上,它有两个明显的特征:一方面,它是建立在知识不完全下的推理,另一方面,它是封闭的,即当公理及推理规则一旦给定之后,人们从一个形式系统中能学到的全部知识已隐藏在公理及推理规则中,在形式系统内部不能描述公理的增加和修改。
但是,人脑的大部分思维活动是在知识不完全的情况下,在不断探索中完成的。现有人工智能的推理具有一定的局限性,尽管为了让机器能模拟人类的思维活动,人们发展了不少不确定性推理模型,但大多缺乏人类处理问题的变通性和创造性。而以可拓性为基础的可拓推理,在形式化和模拟人类思维的变通性方面将是一种具有创造能力的推理方法[22,23]。
可拓推理使人们可以利用可拓性推导出原概念更多的内涵,为人们解决矛盾问题提供了多种思路。可拓推理的核心机制是变换,这与传统推理以蕴含和匹配为核心的机制不同,它的目的是生成、选择恰当的基元去变换原有的基元,从而使矛盾问题得到解决。把可拓推理演绎成可拓算子,然后编制成算法和软件,运用于生成可拓信息或可拓知识,对搜索诊断和数据挖掘等多个领域将有重要的价值。
6 结语
可拓学的理论框架初步建成,可拓学的理论体系远未完成,可拓逻辑的研究刚刚开始。无论在理论研究还是应用研究方面,都有大量的工作要做。在广大可拓学研究者的努力下,相信可拓学将逐步完善和发展,跻身于世界学科之林!
参考文献
[1]蔡文.可拓论及其应用[J].科学通报,1999,44(7):673~682
Cai Wen. Extension theory and its application[J]. Chinese Science Bulletin,1999,44(17):1538~1548
[2]蔡文.可拓集合和不相容问题[J].科学探索学报, 1983,(1):83~97
Cai Wen.Extension Set and Non-Compatible Problems[A]. Advances in applied mathematics and mechanics in china[C],Peking:International Academic Pubishers, 1990:1~21
[3] Wen Cai. Extension Management Engineering and Applications. International Journal of Operations and Quantitative Management, 1999, (1):59~72
[4]蔡文,杨春燕,林伟初.可拓工程方法[M].北京:科学出版社,2000
[5]涂序彦.可拓学——研究“矛盾转化,开拓创新”的新学科[J].中国工程科学,2000,2(12):97
[6]杨春燕,蔡文.可拓工程研究[J].中国工程科学,2000, 2(12):90~96
[7]蔡文.物元模型及其应用[M].北京:科学技术文献出版社,1994
[8]杨春燕.事元及其应用[J].系统工程理论与实践,1998,18(2):80~86
[9]蔡文,杨春燕,林伟初.可拓工程方法(繁体字版)[M].台湾:台湾全华科技图书公司,2001
[10]李和平.可拓学的哲学思考[J].系统工程理论与实践, 1998,18(2): 118~120
[11]杨春燕,吴福芝.可拓集合在资源开拓研究中的应用[J].华南理工大学学报(自然科学版)2001, 29(11):102~104
[12]杨春燕,何斌.可拓方法在新产品构思中的应用,系统工程理论与实践[J]. 1999 , 19(4):120~124
[13]杨春燕,蔡文.可拓集合的新定义[J].广东工业大学学报, 2001, 18(1): 59~60
[14]杨春燕,张拥军,蔡文.可拓集合及其应用研究[J].数学的实践与认识,2002,32(2):301~308
[15]蔡文,杨春燕,何斌.可拓学研究中的若干问题[J].广东工业大学学报, 2001, 18(1): 1~5
[16]左静.基于物元可拓性的物元可拓域[J].郑州工业大学学报, 2001,22(3) :51~52
[17]何斌,王若恩.物元演绎推理[J].系统工程理论与实践,1998,18(1):85~92
[18]程仲棠.现代逻辑与传统逻辑[M].广州:暨南大学出版社,1990
[19]曾繁琨.矛盾化为相容引发的哲学思考[J].广东工业大学学报, 2001,18(1):72~75
[20]何斌,蔡文.物元命题和事元命题[J].广东工业大学学报, 2001,18(1): 88~93
[21]林楠.可拓集合的提升与物元信息模型[J].系统工程理论与实践, 1998,18(1): 93~96
[22]何斌,张应利.可拓学在人工智能中的应用初探[J].华南理工大学学报,1999,27(6):88~92
[23]杨春燕, 李立希, 蔡文.可拓营销策略生成系统(EMSGS)的基本思路与关键技术[R]. 中国人工智能进展,北京:北京邮电大学出版社,2001: 1064~1067
New Development of the Basic Theory of Extenics
Cai Wen, Yang Chunyan, He bin
(Guangdong University of Technology, Guangzhou 510080, China)
[Abstract]The new development of three basic theories of Extenics, including basic element theory, extension set theory and extension logic theory, has been introduced in the paper. And the new theoretical frame of Extenics has also been set forth.
[Key words]Extenics; basic element; extension set; extension logic

