k(x)的背景、用途和使用要求
文[1]- [3]提出了关联函数的基本公式
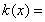
（1）
其中包含了X0和X有公共端点时k(x)的计算方法:
（2）
对于量值的最优值不在X0的中点达到而在点x0达到的情形，[2]和[3]建立了左侧距和右侧距的概念，并规定了相应的关联函数计算公式[4]
=
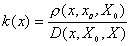（3）
k(x)的建立，使我们能够用公式客观地描述事物具有某种性质的程度，从而排除了人为主观性造成的偏差。
例如，某电机的额定电流值为<10A,20A>，表示了使该电机正常运转所要求的电流强度,假设15A时最优。但是，当电流强度x在<5A,10A>内时，电机仍可勉强运转，低于5A时，电机不会转动。电流强度在<20A,25A>时，电机会过热运转，到25A时，电机烧毁。于是，取X0=<10A,20A>，X=<5A,25A>，用X0和X代入（1），k(x)就表示电流强度x符合要求的程度。
当k(x)³0时，表示这时的电流强度x符合额定要求，即xÎX0；
当-1£k(x)£0时，表示x不符合额定要求，但电机仍能运转，即xÏX0，且xÎX；
当k(x)£-1时，表示x不仅不符合额定要求，而且电机不动或烧毁，即xÏX；
在实际问题中，有很多事情都存在这样两个区间：一个是基本要求的区间X0，一个是质变区间X，当最优点在X0的中点达到时，公式（1）用数量表示了事物符合要求的程度。
使用这一公式时，要注意以下两个问题：
1. 当X0和X有公共端点时，可以使用公式（2）。
2. 若某量值的最优值不在X0的中点达到，而在它的左边或右边x0达到时，则要使用左侧距或右侧距的概念，用公式（3）进行计算。
在个别论文中，没有注意到上述两点要求，错用公式（1），导致了错误的结论，请学者们特别注意。
在可拓学中，利用某变换T，使关联函数值从负值转化为正值，从而定量地描述把矛盾问题转化为不矛盾问题。因此，k(x)是可拓学中重要的基本公式。
参考文献：
[1]蔡文.可拓集合和不相容问题[J].科学探索学报，1983，（10）：83-97
[2]蔡文.物元分析[M].广州：广东高等教育出版社，1987：95-126
[3]蔡文.物元模型及其应用[M].北京：科学技术文献出版社，1994：168-182
[4]张德仲.侧距和相应的关联函数计算公式.http://web.gdut.edu.cn/~extenics/depend03.htm
关联函数有多种形式
关联函数用途很广，因此，在1983-1994年，[1]-[3]就建立了多种类型的关联函数。如：
1、简单关联函数
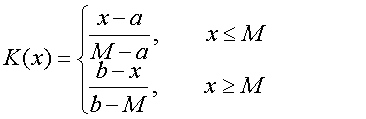
其中，M是量值达到最大值的点，
当M是中点时，有
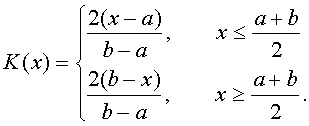
2、初等关联函数
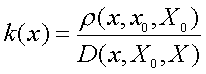
其中，
，x0是量值达到最大值的点。当x0为X0的中点时，
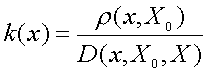
这是最早出现的关联函数的基本公式，它在工程技术上被很多学者使用，并得到很好的效果。
3、二维关联函数（见[2]）
4、n维关联函数（见[2]）
这些公式都适用于该公式假设的条件（范围）内，特别是工程技术领域。
但是，使用这些公式，一定要注意其前提条件，如果用错公式，将会得到错误的结论。
参考文献：
[1]蔡文.可拓集合和不相容问题[J].科学探索学报，1983，（10）：83-97
[2]蔡文.物元分析[M].广州：广东高等教育出版社，1987：95-126
[3]蔡文.物元模型及其应用[M].北京：科学技术文献出版社，1994：168-182
[4]张德仲.侧距和相应的关联函数计算公式.http://web.gdut.edu.cn/~extenics/depend03.htm
公式k(x)对X0和X的要求
关联函数基本公式[1]
（1）
规定XÉX0，根据区间的定义，要求c<a<b<d。因此，不可能出现c>a>b>d的情形，在使用这一公式时，必须注意这一点。
在工程技术中，有可能出现c=a或b=d的情形，这时必须使用公式[2][3]
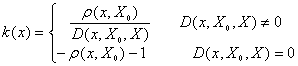
进行计算。
若量值最优点不在X0的中点达到，而在中点的左边达到，或中点的右边达到，则分别采用左侧距或右侧距的概念。而不能用“距”进行计算。同时，
要使用公式
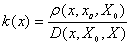
进行计算[2][3]。而不能采用式子（1）进行计算，否则会得到错误的结论。
参考文献：
[1]蔡文.可拓集合和不相容问题[J].科学探索学报，1983，（10）：83-97
[2]蔡文.物元分析[M].广州：广东高等教育出版社，1987：95-126
[3]蔡文.物元模型及其应用[M].北京：科学技术文献出版社，1994：168-182
侧距和相应的关联函数计算公式
文[1]建立了关联函数的基本公式
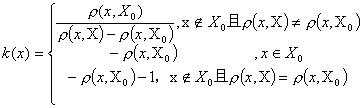
它描述了事物的量值最优点在合格区间X0中点的情形，但是，在社会生活和工程技术中，有很多事件的量值最合适的位置不是在合格区间X0的中点。例如，有的方案要求时间在3-4小时，而3小时是最好的。计算成本时，在5万元-10万元之间，以5万元为最优。再如，某人洗澡时热水的合格区间是<40℃,45℃>，而感到最适宜的是44℃。对于这类最优点不在区间X0中点的现象，计算k(x)时就必须使用公式
，
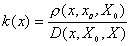这个公式立足于“左侧距”和“右侧距”这两个概念[2][3]，而不是公式（1）的“距”。
定义1：（左侧距）给定区间X=<a,b>，若x0Î(a, (a+b)/2)，称
（1）
为x关于点x0和区间X的左侧距；记为
。
定义2：（右侧距）给定区间X=<a,b>，若x0Î( (a+b)/2，b)，称
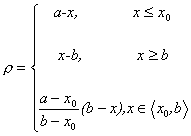
为x关于点x0和区间X的右侧距；记为
。
性质1：若区间X0=<a,b>，X=<c,d>，XÉX0，且无公共端点，x0Î<a,b>，令
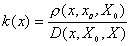
则
(1) xÎX0，且x¹a, b的充要条件是
>0
(2) x=a或x=b的充要条件是=0
(3) xÎX-X0，且x¹a, b,c,d的充要条件是-1<<0
(4) x=c或x=d的充要条件是=-1
(5) xÏX，且x¹c, d的充要条件是<-1
性质2：由性质1所确定的函数在x=x0达到最大值。
在公式（3）中，若X和X0有公共端点xz，则有
性质3：对一切x¹xz，令
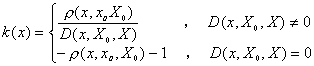
则
(1) xÎX0，且x¹a,b的充要条件是>0
(2) xÎX-X0，且x¹a,b,c,d的充要条件是-1<<0
(3) xÏX，且x¹c,d的充要条件是<-1
(4) 若a=c=xz，
当xzÎX0且xzÏX时，取
=0;
当xzÏX0且xzÎX时，取=-1
当xzÏX0且xzÎX时，取=0Ä(-1)，它表示既等于0，也等于-1。
在使用关联函数公式k(x)时，一定要注意该现象中量值的最优值是在区间X0的中点，还是在区间X0的中点的左边或右边，然后使用相应的公式，错用公式会导致错误的结论，产生不良的影响。
参考文献：
[1]蔡文.可拓集合和不相容问题[J].科学探索学报，1983，（10）：83-97
[2]蔡文.物元分析[M].广州：广东高等教育出版社，1987：95-126
[3]蔡文.物元模型及其应用[M].北京：科学技术文献出版社，1994：168-182
