1引言

可拓学中的关联函数有多种类型，不同的实际问题对应不同的关联函数。在工程技术问题中，利用关联函数去研究实际对象的评价，虽然不是可拓学的核心，但也是可行的。需要指出的是，必须注意不同类型的实际问题要采用不同类型的关联函数，而不能一切实际工程问题都套用同一个公式，这样会得到错误的结论。本文研究了关联函数的构造和零界的确定,为工程技术人员提供可供使用的工具。

2距和位值及相应的关联函数

在经典数学的实变函数中，点x与区间X₀的距离规定为该点与区间内一切点的距离的下确界。因而，不管x在区间X₀内任意位置，点x与区间X₀的距离均为零。这一规定使实变函数无法用来表示同类事物不同元素的区别，也即类内即为同。为了表示事物具有某种性质的程度，描述量变和质变，可拓学引进了距[1]的概念。规定：点x与区间X₀的距为

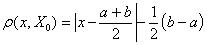
这一规定，就使当点x在区间内时，点x与区间X₀之距为一个负数，位置不同时，其值也不同。以此为基础建立的关联函数将能够表述类内元素具有不同程度的性质。

在大量的实际问题中，对量值的规定有基本要求的区间X₀，也有产生质变的范围X。如对电机有额定电流的规定—区间X₀，也有电机不能运转的电流值到烧毁的值构成的区间X。任何一个值与这两个区间的关系用位置值表示：

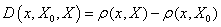
有了距与位置值（简称位值）的概念，文[2]讨论了描述事物具有某种性质的程度的关联函数[2]

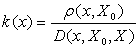
这个关联函数是最初等的关联函数，它的最大值在X₀的中点达到。

3侧距和相应的关联函数计算公式

在社会生活和工程技术中，有很多事件的量值最合适的位置不是在合格区间X₀的中点。例如，有的方案要求时间在3-4小时，而3小时是最好的。计算成本时，在5万元-10万元之间，以5万元为最优。再如，某人洗澡水的温度适宜区间是<40℃,45℃>，而感到最适宜的是44℃。有的实际问题要求时间越少越好，有的老板希望利润和工程质量越高越好。文[1]针对这类问题，建立了侧距的概念，并利用侧距建立符合上述要求的关联函数计算公式。

定义1：（左侧距）给定区间X=<a,b>，若x₀Î(a, (a+b)/2)，称

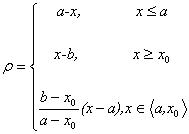
为x关于点x₀和区间X的左侧距；记为。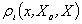

定义2：（右侧距）给定区间X=<a,b>，若x₀Î( (a+b)/2，b)，称

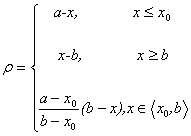
为x关于点x₀和区间X的右侧距；记为。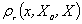

性质1：若区间X₀=<a,b>，X=<c,d>，XÉX₀，且无公共端点，x₀Î<a,b>，令

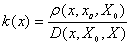
则

(1) xÎX₀，且x¹a, b的充要条件是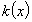>0

(2) x=a或x=b的充要条件是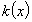=0

(3) xÎX-X₀，且x¹a, b,c,d的充要条件是-1<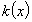<0

(4) x=c或x=d的充要条件是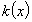=-1

(5) xÏX，且x¹c, d的充要条件是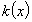<-1

性质2：由性质1所确定的函数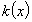在x=x₀达到最大值。

4区间X₀和X有公共端点时的关联函数计算公式

在实际问题中，还有一些问题，X₀和X有公共端点，如长、宽、高的取值，有时左端点都取0，对于X₀和X有公共端点的问题，又必须建立相应的关联函数计算公式。

在性质1中，若X和X₀有公共端点x_z，则有

性质3：对一切x¹x_z，令

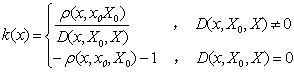
则

(1)xÎX₀，且x¹a,b的充要条件是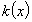>0

(2) xÎX-X₀，且x¹a,b,c,d的充要条件是-1<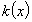<0

(3)xÏX，且x¹c,d的充要条件是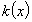<-1

(4)若a=c=x_z，

当x_zÎX₀且x_zÏX时，取=0;

当x_zÏX₀且x_zÎX时，取=-1

当x_zÎX₀且x_zÎX时，取=0Ä(-1)，它表示既等于0，也等于-1。

在使用上述关联函数公式k(x)时，一定要注意该问题中量值的最优值是在区间X₀的中点，还是在区间X₀的中点的左边或右边，X₀和X有无公共端点，然后使用相应的公式。错用公式会导致错误的结论，产生不良的影响^[4]。另外，随着多因素等问题的提出，还可建立相应的关联函数。

5用关联函数描述量变和质变

一物，关于某一固定的特征，有相应的量值。当量值在一定范围内改变时，该物某性质特征的量值不发生明显的变化。但超过一定范围时，该性质特征的量值将会发生变化。例如，H₂O的温度在0℃—100℃变化时，它的状态特征的量值是液态。超过这个范围，就不是液态，而是气态或固态。为了描述这种量变与质变的现象，可拓学中利用上述关联函数计算公式，建立了“节域”和“质度函数”的概念^[3]。它们描述了客观事物由量变到质变的辩证规律。节域概念表达了事物的某性质对应的量值的范围，当量值在节域的范围内变化时，事物的性质就保持着它的稳定性。当事物某量值的变化超越节域时，就会引起该性质向另一种性质的转化。可拓学中的发展变换、受迫变换与双否变换都反映了在事物的运动过程中，事物的某些性质与相应量值的相关规律。

能够用形式化清楚地描述质量互变规律，是可拓学的一个重要功能。正是由于可拓学具有这一功能，它就能够为描述事物的量变和质变提供可拓模型。

可拓集的核心概念是质变域[3]，质变域有正质变域和负质变域之分。正质变域表示经典集的非域或论域外一部分元素，它们不具有某种性质，但由于可拓变换（包括元素本身的变换、关联函数的变换和论域的变换），变为具有该性质。显然，不同的变换具有不同的质变域。质变域中的元素，经过变换产生了质变。质变域的提出，使人们把矛盾问题转化为不矛盾问题具有合理的理论基础。

在文[1]的可拓集定义2.23中，当T=e时，可把论域U划分为三部分：

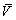={u∣u∈U,k(u)<0 }，={u∣u∈U,k(u)>0 }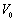，={u∣u∈U,k(u)=0 }，

分别称为论域U的正域、负域和零界。

当T≠e时，以T_U=e，T_k=e,T_u≠e为例，可把论域U划分为五部分，相应于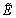(T)的四个域和拓界，这五部分分别记为

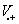= {u∣u∈U,y=k(u)≤0 ,y’=k(T_uu)>0}

称为论域U关于变换T_u的正质变域（文[1]中称为正可拓域）；

= {u∣u∈U,y=k(u)≥0 ,y’=k(T_uu)<0}

称为论域U关于变换T_u的负质变域（文[1]中称为负可拓域）；

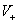= {u∣u∈U,y=k(u)>0 ,y’=k(T_uu)>0}

称为论域U关于变换T_u的正量变域（文[1]中称为正稳定域）；

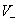= {u∣u∈U,y=k(u)<0 ,y’=k(T_uu)<0}

称为论域U关于变换T_u的负量变域（文[1]中称为负稳定域）；

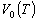= {u∣u∈U,y’=k(T_uu)=0}

称为论域U关于变换T_u的拓界。

由此可见，可拓集可以定量化地表达事物的转化，利用它可以对事物进行变化的分类。

6零界的确定

事物关于某特征的量值变化的临界点是具有某种性质的量值和不具有某种性质的量值的公共点，也即产生质变的点。在这一点上，量值既符合要求，也不符合要求。物既具有某种性质，又不具有某种性质。例如，H₂O关于温度的值0℃和100℃就是这样的临界点。可拓集合的零点正好恰当地描述这类临界点。可拓集合中以关联函数值为零的点来表示这种质变的点，并称为零点，所有零点的全体称为零界。

零界描述了客观世界中处于临界状态的事物。可拓集中的零界有两种类型：1）零界不是空集；2)零界是空集。下面分别予以介绍。

6．1零界不是空集

在客观世界里，有的质变过程存在既是又非，既不是，又不非的事物，即临界事物。例如，在海平面的H2O,当温度处于100C时，既使水，又不是水；既是水蒸气，又不是水蒸汽。8月1日0时，既是7月的最后一刻，又是8月的最初一刻。100C的H2O和7月31日24时称为临界。处于临界状态的元素是临界元素。在建立了关联函数以后，临界元素的关联函数值为零，它们的全体称为零界。这时，论域被分为图1中的正域、负域和零界三个部分。当实施文[1]的定义2.23中的变换T时，临界元素所处的位置会产生改变。例如，如果把H2O的位置从海平面变换到青藏高原。临界是80C的H2O,这时85C的H2O是水蒸汽，而不是水。当考虑时间的地点从北京变到乌鲁木齐时，8月1日2时，既是7月的最后一刻，又是8月的最初一刻。这时，临界是8月1日2时。北京时间8月1日1时还记为乌鲁木齐7月31日。由此可见，变换使临界的位置改变，也使其他元素的位置改变。这就是图2所表示的，变换使事物转化。变换实施后，关联函数值取零的元素的全体称为拓界。

对于基元可拓集，假如论域是，建立关联函数k(v)以后，对于基元B=(O,c,V)，当V取值为一个数v时，可以根据关联函数值k(v)的值决定B属于哪个域，如果k(v)=0，则该基元属于零界。如果V取值是一个区间<a,b>，基元的关联函数值也对应一个区间为<k(a),k(b) >,若k(b)<0,则B是负域的元素；若k(a)>0,则B是正域的元素;当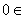<a,b>时，则该基元为零界元素。

例如，房子的门口有一个门槛，门槛之内的人为“房子里的人”，门槛之外的人为“房子外的人”。那么，横躺在门槛上的人是“房子里的人”，还是“房子外的人”呢？在这个例子中，如果以门槛中线为界，中线内的点的关联函数值取正数，中线外的点的关联函数值为负数。由于横躺在门槛上的人的位置是一个区间，因此对应的关联函数值也是一个区间，身体与门槛中线接触的点的关联函数值为零。这时的基元（人A,位置，V）的关联函数值是一个区间，该区间包含零点，因此，该基元是零界元素。显然，门内多一点的人和少一点的人都是零界元素，但它们对应的关联函数值的区间是不同的。抽象地说，零界元素也是有区别的，它们以其对应的关联函数值区间作为区别的依据。

6．2零界是空集

在客观世界里，有的论域只分为具有某种性质和不具有某种性质，符合要求或不符合要求。康托集就是建立在这样的分类基础的。例如，学生考试时，以60分为合格，考试成绩为60分和60分以上的学生都是合格的，不足60分的学生都是不合格的学生。不存在又合格又不合格的学生。对于这样的客观事物，康托集把论域只分为两类：A和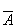。论域中的一个元素，要么属于A，要么属于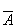，两者只居其一，且必居其一。这时，零界是空集。在某一变换下，A中的元素可以变为属于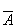的元素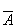，中的元素有的也会变为A中的元素。

6．3拓界

与零界相仿，拓界也有类似零界的两种情形：拓界是空集和拓界不是空集。读者可自行研究。

7文[5]和[6]的错误以及产生错误的原因

（1）文[5]中关于关联函数有错的提法和证明是错误的

文[5]中反复强调，公式

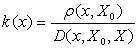
有错误，并做了证明。事实上，其证明是错误的。

在文[5]中，作者指出上述关联函数在（2）和（4）的假设下是错误的。经多次核实表明，其原因是文[5]作者在代数计算中产生错误造成的。

该文约束条件（2）是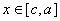：,；,于是有ρ（x,X0）=a-x,ρ（x,X）=x-d,所以，

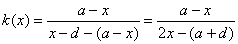
由于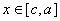,故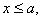，又因为a<d,故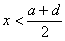，所以，,因此，k(x)有意义。

类似地，对于文[5]中的假设（4），有，由（4）的假设，c+b-2x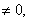因此，k(x)有意义。同样道理，（6）和（8）的情形下，k(x)也是有意义的。

（2）文[5, 6]中把工程界有人错用公式渲染为可拓学的错误是不妥的

文章[5,6]把应该用“侧距的关联函数计算公式”错用了“最大值在区间中点达到的距的关联函数计算公式”，进而导致了错误的结论。把专业领域中这种用错公式的个案进行渲染，断言“可拓学不能在实际工程应用”，未免过于牵强。早在1987年出版的《物元分析》和1994年出版的《物元模型及其应用》中，对距和侧距以及相应的关联函数公式都作了规定和证明，对于不在X₀中点达到的情形，需要应用基于侧距的关联函数公式

_。

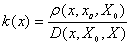物关于某特征的量值在一定范围内变化时，物的变化只是量的改变，当超出一定范围时，会产生质变。可拓集合的关联函数用形式化和定量化的方法描述物的量变和质变。在可拓集合中，量变域和质变域表示了时间变换下物的量变和质变的范围。

（3）用可拓集合中的零点来描述临界点是符合辩证逻辑的

用可拓集合中的零点来描述临界点是从本质上描述事物的临界状态，从6关于零界的确定可以看到，可拓学中用零界描述客观事物中的临界点的全体是符合辩证逻辑的。

参考文献：

[1]杨春燕蔡文.可拓工程[M].北京：科学出版社，2007.8.

[2] CAI Wen. Extension theory and its application[J]. Chinese Science Bulletin，1999,44（17）：1538-1548.

[3]蔡文.,杨春燕,陈文伟，李兴森可拓集与可拓数据挖掘[M].北京：科学出版社，2008.

[4]陈薇.基于关联函数评价应注意的问题[J].哈尔滨工业大学学报，2006，38（7）：1143-1145.

[5]陈守煜.工程可变模糊集理论与模型-模糊水文水资源学数学基础[J].大连理工大学学报，2005，45(2)：308-312.

[6]陈守煜.可变模糊集理论的哲学基础[J].大连理工大学学报(社会科学版)，2005，26（1)：53-57.