《大连理工大学学报》2005年第2期发表了陈守煜教授的论文“工程可变模糊集合理论”,提出证明了可拓集合和关联函数的错误。2007年第4期又在“资深教授学术论文专栏”发表了陈守煜教授的论文“可变模糊集合理论——兼论可拓学的数学与逻辑错误”[2],该文重复了前文的内容和结论。
经过反复论证,表明陈教授的证明和结论有误[3]:
错误一.该文618页左栏倒数第2行说:“可拓学的数学逻辑基础可拓集合存在数学与逻辑错误,关联函数基本公式存在两种错误形式,关联函数侧距公式同样存在错误,因而在实际领域,尤其在工程领域应用中出现了大范围的错误,本文将对此作专门的论述。”
这个结论不对。
理由:1.可拓集合是继康托集合和模糊集合之后提出的对事物进行可变分类的集合基础,由于康托集合和模糊集合是对事物的静态分类,无法描述事物“从非变为是”或“从是变为非”的情形,因此,也就无法作为解决矛盾问题的基础,为此,需要研究变换下的分类,从而建立了可拓集合。
2004年,中国科学院吴文俊院士和中国工程院李幼平院士为首的鉴定委员会对“可拓论及其应用研究”所做的鉴定指出:“可拓集合理论是在康托集合与模糊集合之后的一项创造,它对实变函数中距离的概念加以拓展,引入描述客观事物性质变化的关联函数工具,为表达矛盾问题的转化提供了定量手段;可拓逻辑则是辨证逻辑和形式逻辑的科学集成。”
2005年12月,由科技部、教育部、中国科学院、中国工程院、国家自然科学基金委员会、国防科工委和解放军总装备部联合组办的“香山科学会议”在北京香山饭店召开以“可拓学的科学意义与未来发展”为主题的学术讨论会,会议指出,“可拓学突破了康托集合、模糊集合和经典逻辑的局限,建立了可拓集合、关联函数、可拓逻辑和可拓方法,初步形成了描述和处理量变与质变问题的能力,建构了矛盾问题智能化处理的理论体系和应用方法。”
由于可拓学是研究通过变换处理矛盾问题的学科,可拓集合不是建基于经典数学的康托集合的基础上,因此,它不属于数学。它的逻辑基础是可拓逻辑,而不是数理逻辑。
谈可拓学的数学逻辑错误之前必须弄清“可拓学是干什么的”,可拓集合与康托集合、模糊集合的区别与联系,可拓逻辑与数理逻辑的区别与联系。
2.可拓学的核心是通过变换处理矛盾问题,在处理矛盾问题的过程中,对提出的大量策略需要进行评价,而不是专门研究评价的。其评价方法也可以用于其他领域,但必须准确应用相应的公式,而不能不管背景套用一个公式。有个别工程技术人员由于没有掌握好这一点,用错了公式,造成了他所应用的具体问题出现错误,但个别人用错可拓学公式的错误归结为可拓学的错误,说是大面积的错误,是不合适的。就如一个学生用错数学公式解错了应用题,不能上纲为数学的错误一样。
近年,在计算机、设计、管理、控制、检测和中医药等领域利用可拓论和可拓方法的应用取得较好的成果。国家自然科学基金委员会已资助有关可拓学的研究项目30项;并研制了若干可拓软件,申报了专利。
对“可拓论及其应用研究”所做的鉴定指出:“本项目为计算机帮助工程领域处理矛盾问题提供了基础理论和基础方法。目前,已经在控制与检测、人工智能与计算机、经济与管理等领域得到初步的应用[4],表明可拓学方法在工程技术领域将有广阔的应用前景。”
“香山科学会议”指出:“可拓学与其它学科交叉融合,初步取得了一批工程应用的实际效果,展现了广阔的应用前景。”
由上述成果可见,说可拓学不能在工程应用是杜撰的,缺乏根据的。
值得商讨的提法:该文620页左栏第10行说:“可拓集合在数学定义中已经明确规定:关联函数k(x)前面的正负号‘+’、‘-’号作为定性之用,……但是,在可拓集合中,却又把关联函数k(x)前面的正负号‘+’、‘-’号作为可拓集合运算之用”。
这句话不准确。为什么作为定性之用就不能进行运算呢?缺乏根据。
二.该文620页左栏倒数第16行说:“出现了类似于a>b,b>c,c>a不能允许的数学与逻辑错误,可拓学论著充斥着这样的数学与逻辑错误”
这个结论不对。
未见指出在何处出现这种情况。
三.该文620页左栏倒数第14行说:“文献[28]中的综合关联函数定义…..是近期可拓学可拓集合并、交运算数学与逻辑错误的典型例子”。
这个结论不对。
理由:从可拓学的体系看,文献[28]中的综合关联函数定义…是正确的,文中已做了介绍,可以看原文。
产生错误的原因:不同的科学体系有不同的规定,可拓逻辑与数理逻辑有一定的区别。
四.该文621页右栏倒数第27行说:“在可拓集合关联函数k(u)=0或可拓集合零界概念的定义下,出现了这个‘客观存在’的人‘不存在’了的逻辑矛盾,违背了形式逻辑中的一条基本规律——不矛盾律。”
这段话不对。
理由:
1.这个‘客观存在’的人就是u,其关联度为零。这是函数的规定。
2.可拓集合的逻辑基础是可拓逻辑,不是形式逻辑,因此不必符合形式逻辑规律的要求,作者需要了解一点“科学学”。
五.该文621页右栏倒数第20行说,“可拓集合的定义零界关联函数k(u)=0违背了形式逻辑的不矛盾律,因而在数学逻辑上都有误。因此,以关联函数k(u)=0为基础的可拓集合定义是错误之源。”
这段话不对。
理由:
1.“可拓集合的定义零界关联函数”的提法不通。
2.k(u)=0是指在关联函数k(u)中,元素u的关联函数值为0,不是关联函数,更不是零界关联函数。
3.可拓学的逻辑基础是可拓逻辑,不是形式逻辑,要服从的是可拓逻辑的规律,而不是形式逻辑的规律。
4.关联函数k(u)=0的提法不妥。关联函数是y=k(u),或简记为k(u)。k(u)=0应是关联函数值。必须与“函数”,“函数值”,“定义”等概念一致。
5. 根据1-4,表明,“以关联函数k(u)=0为基础的可拓集合定义是错误之源”,这句话不妥。可拓逻辑和可拓集合的规定不是这样的。
六.该文622页右栏第10行例3中k(x)=-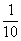 有误。
有误。
经核实,这个数字没有错。
七.该文622页右栏倒数第15行例4中k(x)=-0.3684有误。
经核实,这个数字没有错。
八.该文621页右栏倒数第1行至623右栏第3行有很多处提到关联函数或可拓集合的数学逻辑错误。
这些结论不对。
经过反复核查,证明关联函数或可拓集合没有错,所提的错误都是来源于作者的第一篇文章不当造成的,请参阅“评‘工程可变模糊集合理论与模型——模糊水文水资源数学模型’一文中的错误”,不再重复列出。
参考文献:
[1]陈守煜.工程可变模糊集理论与模型-模糊水文水资源学数学基础[J].大连理工大学学报,2005,45(2):308-312.
[2]陈守煜.“可变模糊集合理论——兼论可拓学的数学与逻辑错误”[J].大连理工大学学报,2007,47(4)
[3]陈薇.基于关联函数评价应注意的问题[J].哈尔滨工业大学学报,2006,38(7):1143-1145.
[4]杨春燕蔡文.可拓工程[M].北京:科学出版社,2007.8.

