《大连理工大学学报》2005年第2期发表了陈守煜教授的论文“工程可变模糊集合理论与模型——模糊水文水资源数学模型”[1],提出证明了可拓集合和关联函数的错误。经过反复论证,表明陈教授的证明和结论有误:
错误一.该文310页右栏倒数第8行说:“关联函数(20),即
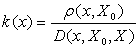
是错误的”,这一结论不对。
理由:函数(20)是一个计算式,不是定理。这一公式只要分母不为零就可以计算,而式子给定的条件是X0与X无公共端点,保证了分母不为零。因此这一式子不存在错误的问题。对于X0与X有公共端点的情形,1994年出版的专著《物元模型及其应用》,早对各种特殊情形作了明确的规定,使k(x)成立。
二.该文311页左栏第9行指出“关联函数(20)只有在约束条件(1)(3)才有意义,当出现约束条件(2)时,关联函数(20)有误”,这个结论不对。
理由:兹证明如下:
该文约束条件(2)是: ,
,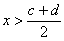 ;,于是有ρ(x,X0)=a-x,ρ(x,X)=x-d,所以,
;,于是有ρ(x,X0)=a-x,ρ(x,X)=x-d,所以,
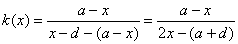
由于 ,故
,故 ,又因为a<d,故
,又因为a<d,故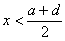 ,所以,
,所以,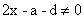 ,因此,k(x)有意义。
,因此,k(x)有意义。
三.该文311页左栏第9行指出“关联函数(20)只有在约束条件(1)(3)才有意义,当出现约束条件(4)时,关联函数(20)有误”,这个结论不对。
理由:兹证明如下:
该文约束条件(4)是:
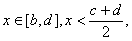
于是有ρ(x,X0)=x-b,ρ(x,X)=d-x,于是,
 ,
,
由于 故
故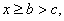 故
故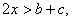 所以,
所以,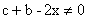 ,因此,k(x)有意义。
,因此,k(x)有意义。
值得商讨的提法一:该文310页右栏倒数第6行“证明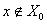 的关联函数式(20)的条件性”。“证明……条件性”这种提法有语病的问题,也有逻辑的问题,函数式与定理是不同的。
的关联函数式(20)的条件性”。“证明……条件性”这种提法有语病的问题,也有逻辑的问题,函数式与定理是不同的。
原因:对函数的概念理解不准确,对“证明”是什么的内涵理解不准确。
值得商讨的提法二:该文311页左栏第7行:“只有当 与
与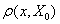 在相同区间的约束条件下,关联函数(20)才是正确的”
在相同区间的约束条件下,关联函数(20)才是正确的”
这句话不明确。相同区间是指什么?相同区间的约束条件是指什么?没有说清楚。
值得商讨的提法三:该文311页左栏第11、12、13、14行式子(25)(26)的写法不规范。
值得商讨的提法四:该文311页左栏第17行“证明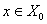 的关联函数式(20)的条件性”,同“值得商讨的提法一”,从略。
的关联函数式(20)的条件性”,同“值得商讨的提法一”,从略。
四.该文311页左栏倒数第2行指出“当出现约束条件(6)时,关联函数(20)有误”,这个结论不对。
理由:与一的证明相仿,依然可以证明k(x)有意义。
五.该文311页左栏倒数第2行指出“当出现约束条件(8)时,关联函数(20)有误”,这个结论不对。
理由:与一论述相仿,从略
六.该文311页左栏第8行指出“由式(21)、(23)与(21)、(21)可见,关联函数(20)只有在约束条件(1)(3)下才有意义”,这个结论是错误的。
理由:函数有三个要素:定义域、变化规则和值域。当给出定义域中的一个自变量时,按照变化规则,值域中有因变量与之对应。该文的证明不符合函数的定义。
七.该文311页左栏第19行指出“即x点落在M点的左侧时,建立区间[a,M]上的关联函数才有意义”,这个结论不对。
理由:同六的分析。
八.该文311页左栏倒数第13行的式子(27)前面讨论了M是关联函数的最大值点,那么式子(27)就应该用侧距的公式来讨论,而不是用式子(27)。
九.该文311页左栏倒数第6行的式子(28)前面讨论了M是关联函数的最大值点,那么式子(28)就应该用侧距的公式来讨论,而不是用式子(28)。
十.该文311页左右栏第4行的“以关联函数k(x)>0和k(x)<0作为事物具有或不具有性质P的判断依据,是对事物的一种表象化描述,割断了事物矛盾运动变换过程中对立统一双方及其相互转化的内在联系”这一观点不对。
理由:忽略关联函数中还有k(x)=0的作用,并没有割断…联系。
十一.该文311页左右栏倒数第16行“关联函数k(x)公式(20)是错误的,遗漏了重要约束条件,不能在实际工程中应用。”
这一结论不对。
理由:由于一至十,所以“关联函数的错误”这一断言是不对的。
参考文献:
[1]陈守煜.工程可变模糊集理论与模型-模糊水文水资源学数学基础[J].大连理工大学学报,2005,45(2):308-312.
[2]陈守煜.“可变模糊集合理论——兼论可拓学的数学与逻辑错误”[J].大连理工大学学报,2007,47(4)
[3]陈薇.基于关联函数评价应注意的问题[J].哈尔滨工业大学学报,2006,38(7):1143-1145.
[4]杨春燕蔡文.可拓工程[M].北京:科学出版社,2007.8.

